Hi,
To adapt the book example to Alloy 6 it takes a bit more work. Alloy 5 did not had an implicit notion of state nor support for mutable relations. This means that we needed to model the state of the system explicitly. In the “Software Abstractions” example, signature Book was actually being used to model the different states of a single address book, not different address books. In Alloy 6 we don’t need to model the system state explicitly so and we can declare fields and signatures to be mutable, so we can just have the following declarations.
sig Name {
var addr : lone Addr
}
sig Addr {}
We have names and addresses and add is a mutable field that associates each name with its address, if any. Now, to model add we can do the following.
pred add[n: Name, a: Addr] {
addr' = addr + n -> a
}
The prime operator show be applied to mutable expressions (namely mutable fields) and determines the value of that expression in the next state. If you apply it to a non-mutable expression it has no effect. Here we say that in the next state the pair n->a will be added to the current value of addr. You can ask for an “interesting” example of this predicate with the following command.
pred showAdd[n: Name, a: Addr] {
add[n,a]
#addr' > #addr
}
run showAdd for 3 but 2 steps
Notice the scope 2 steps which states that we are only interested in seeing the first two states of execution. The predicate is only imposing that predicate add should be true in the first state, so there is no point in looking at more than two states because no restrictions are being imposed on what happens afterwards, so the trace will be more or less random. The result of this command could be the following.
Similar to what was done in “Software Abstractions” we can now model del and check the assertion that delete undoes add as follows.
pred del[n: Name, a: Addr] {
addr' = addr - n -> a
}
assert delUndoesAdd {
all n: Name, a: Addr |
add[n,a] and after del[n,a] implies addr'' = addr
}
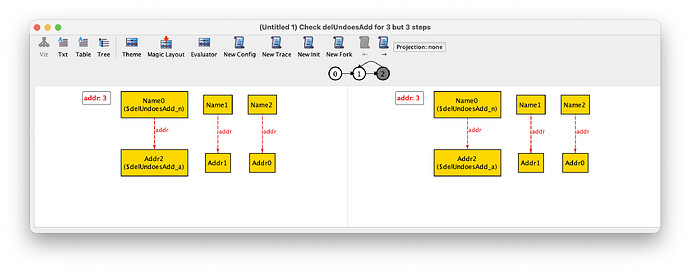
check delUndoesAdd for 3 but 3 steps
Notice the use of the after temporal operator, which is true for a formula if that formula holds in the next state. In this case we want to check that if add happens in the first state and del in the second (the next) state, then the value of addr in the third state is equal to the value of addr in the first state. Since we need three states to reason about this property we set the scope of 3 steps. As mentioned in the book, this assertion is not valid and a possible counter-example is the following.
Notice that to see what is happening in the transition between the second and third state (as shown in the second picture above) we need to press right arrow button.
I hope this helped. I recommend you take a look at https://practicalalloy.github.io to learn a bit more about Alloy 6, in particular about all the new temporal operators and how to model a state machine with those operators.
Best,
Alcino